해시(Hash)
데이터를 효율적으로 관리하기 위해 임의의 길이 데이터를 고정된 길이의 데이터로 매핑
- 해시 함수: 데이터를 효율적으로 관리하기 위해 임의의 길이의 데이터를 수학적 연산을 통해 고정된 길이의 데이터로 매핑하는 함수이다. 해시 함수에 의해 얻어지는 값을 해시 코드, 해시라고 한다.
- 해시 테이블: 키와 값을 매핑해둔 데이터 구조이다. 해시 함수로 얻은 해시를 키로 활용하여 index로 사용하고 해당 index에 데이터를 저장하여 효율적인 검색을 위해 사용된다.
해시 순서
- 해당 원소의 해시 함수를 이용하여 해시값을 얻는다.
- 해시값을 주소로 하는 위치에 원소를 저장한다.
- 저장 후 검색 시에도 원소의 해시값으로 계산하여 해당 위치로 이동한다.

추상 자료형 사전구조
- 인터페이스와 기능 구현을 분리한 자료형
- 기능 구현구분을 명시하지 않아 사용 시에는 기능이 어떻게 돌아가지 몰라도 되는 편리함을 가진다.
- 대표적으로 스택 큐 연결리스트 딕셔너리
- 해시 테이블은 인터페이스만을 보았을때는 데이터 식별자로 숫자 뿐만아니라 문자열 파일등을 받아와 Value를 연상
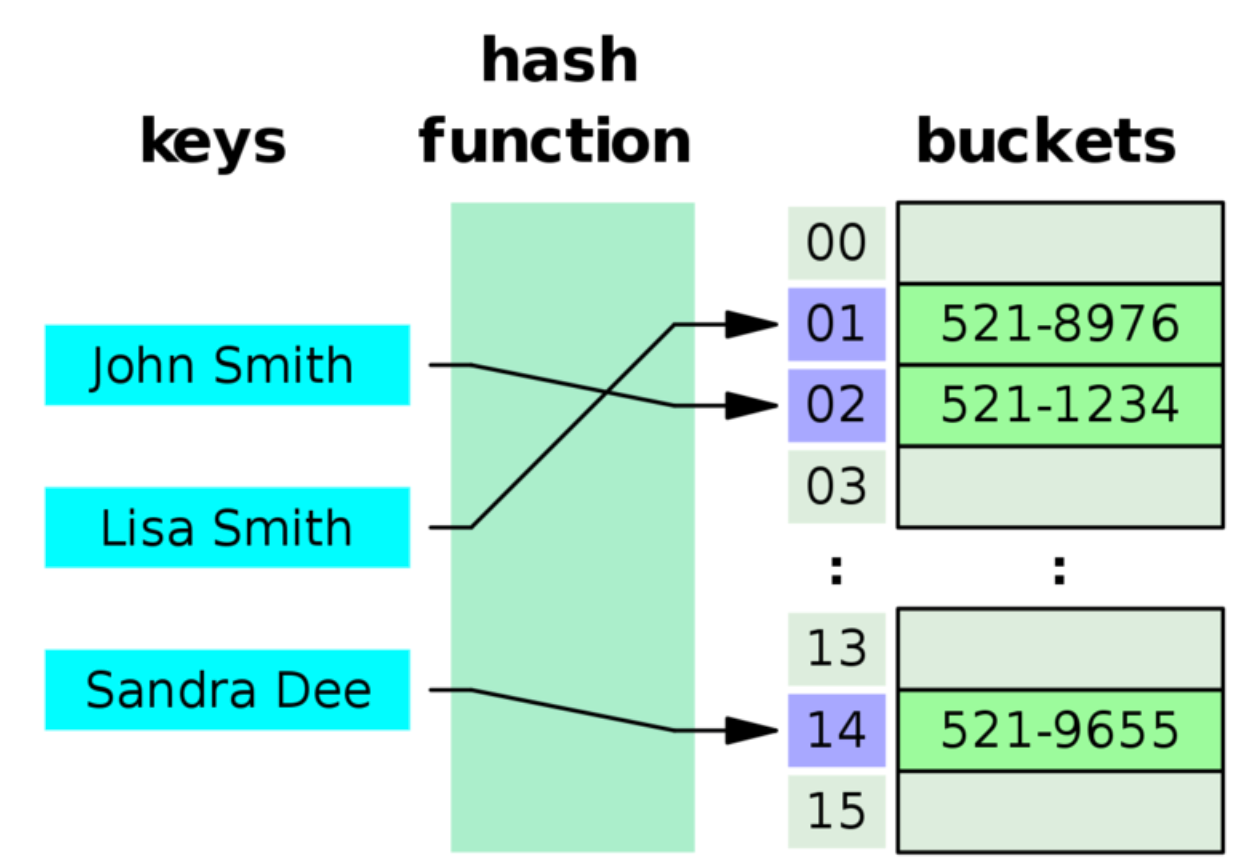
해싱의 구조
- 어떤 항목의 탐색 키만을 가지고 바로 항목이 저장되있는 배열의 인덱스를 결정하는 기법
- 탐색키를 작은 정수로 매핑 시키는 함수가 필요
- 예를들어 영어사전에서는 단어가 탐색키가 되고 이 단어를 해싱 함수를 이용하여 적절한 정수 i로 변환한 다음, 배열 요소 ht[i]에 단어의 정의를 저장하는 것

해시 테이블의 구조
- 해시테이블은 n개의 버킷으로 이루어지는 테이블로서 n-1개의 원소를 가진다.
- 하나의 버킷은 s개의 슬롯을 가질 수있으며, 하나의 슬롯에는 하나의 항목이 저장됨
- 하나의 버킷에 여러개의 슬롯을 두는 이유 - 서로 다른 두 개의 키가 해시 함수에 의해 동일한 해시 주소로 변활 될 수 있으므로 여러 개의 항목을 동일한 버킷에 저장하기 위함

버킷과 슬롯
버킷
- 여러개의 슬롯을저장하는 레코드 형태의 자료 구조
- 버킷의 갯수는 고정적
슬롯
- 해시와 매핑되는 값이 저장되어 있는 공간
- 하나의 버킷 안에는 여러개의 슬롯이 존재할 수 있음
- 슬롯은 하나이상의 값을 저장할 수 있음
해시 테이블이 사용되는 이유
- 평균적으로 탐색, 삽입, 삭제에 O(1)의 시간 복잡도를 가짐
- 어떤 항복과 다른 항목의 관계를 모형화하는데 좋다.
- 무한한 데이터를 유한한 키값으로 관리할 수 있다.
실제의 해싱
- 해시 테이블의 크기가 제한되어있으므로 하나의 탐색키당 해시 테이블에서 하나의 공간을 할당 할 수가 없음
=> 해싱함수가 필요 - 충돌과 오버플로우 발생
=> 슬롯의 숫자도 무한이 아니기 때문, 해싱함수에서 나온 결과가 같을 경우 충돌 발생
해시충돌
다른 내용의 데이터가 같은 키를 갖는 상황.
같은 키 값을 가지는 데이터가 생기는 것은 특정 키의 버켓에 데이터가 집중된다는 뜻. 너무 많은 해시 충돌은 해시 테이블의 성능을 떨어뜨린다.
- 해시함수의 입력값은 무한하지만 출력값의 가짓수는 유한하므로 해시충돌은 반드시 발생 (*비둘기집 원리)
- 클러스터링(Clustering) : 연속된 레코드에 데이터가 몰리는 현상
- 오버플로우(Overflow) : 해시 충돌이 버킷에 할당된 슬롯 수보다 많이 발생하면 더 이상 버킷에 값을 넣을 수 없는 현상
*비둘기집 원리 : n+1개의 물건을 n개의 상자에 넣은 경우, 최소한 한 상자에는 그 물건이 반드시 두 개 이상 존재
충돌 해결방법
1. 체이닝
- 버킷 내에 연결리스트를 할당하여 버킷에 데이터를 삽입.
- 해시 충돌이 발생하면 연결리스트로 데이터들을 연결
- 체이닝의 경우 버킷이 꽉 차더라도 연결리스트로 계속 늘려가기에 데이터의 주소값은 바뀌지 않는다.
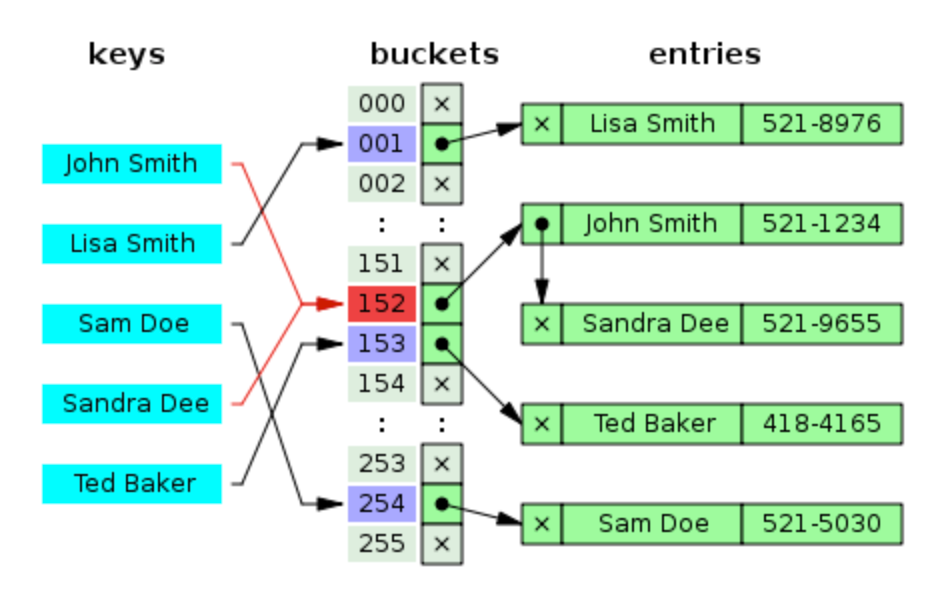
2. 개방 주소법
- 해시 충돌이 일어나면 다른 버킷에 데이터를 삽입하는 방식 (데이터의 주소값이 바뀜)
- 삭제의 경우 충돌에 의해 저장된 데이터가 검색되지 않을 수 있음
=> 삭제한 위치에 더미노드를 삽입 (다음 위치까지 연결 해 주는 역할) - 더미 노드가 많아지면 버킷을 연속적으로 검색해야 하기 때문에
더미 노드의 개수가 일정 이상이 되었을경우 주기적으로 새로운 배열을 만들어 재해시를 해줘야 성능을 유지 가능
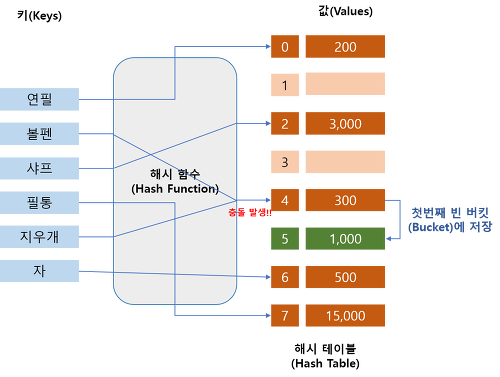
2.1 선형 탐색
- 해시 충돌시 다음 버킷, 혹은 몇 개를 건너뛰어 데이터를 삽입
- 장점 : 구조가 간단하고 캐시의 효율이 높음
단점 : 최악의 경우 해시테이블 전체를 검색해야 하는 상황이 발생, 데이터의 클러스터링에 가장 취약
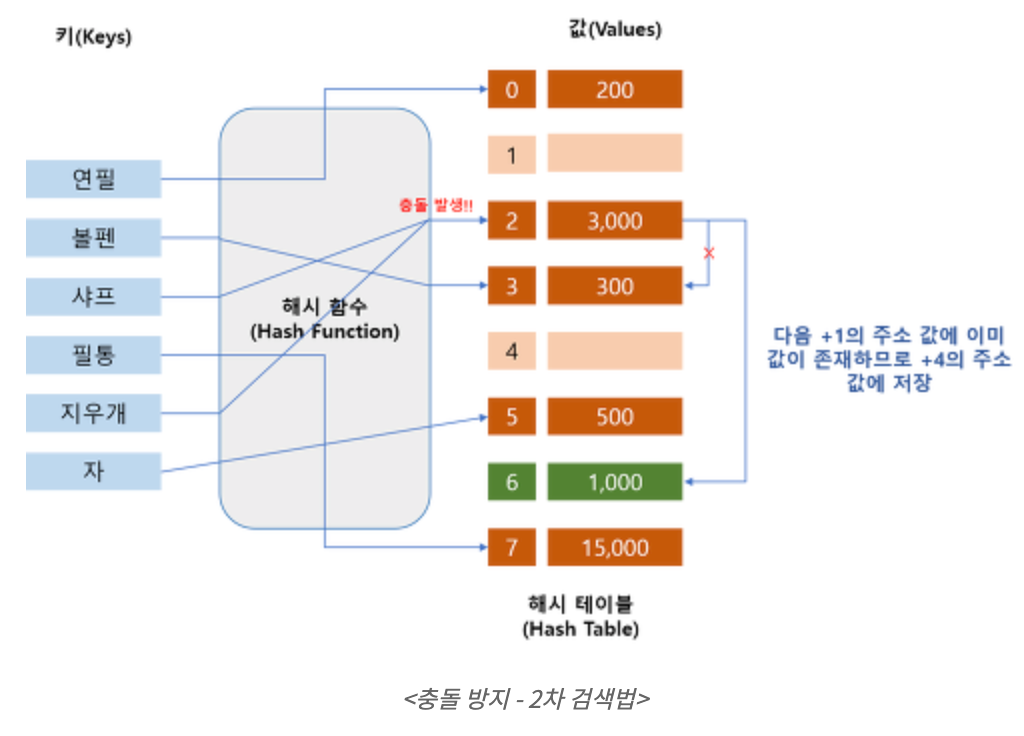
2.2 2차 검색법
- 원래 저장할 위치로부터 떨어진 영역을 차례대로 검색하여 첫번째 빈 영역에 키를 저장하는 방법
- 선형 검색법에서 발생하는 제1 밀집문제를 제거하는 방법
- 같은 해시값을 갖는 키에 대해서는 제 2 밀집 발생
- 캐시 효율과 클러스터링 방지 측면에서 선형 검색법과 이중 해싱의 중간정도의 성능
2.3 이중 해시
- 해시 충돌시 다른 함수를 한번 더 적용한 결과를 이용
- 캐시 효율은 떨어지지만 클러스터링에 영향을 거의 받지 않음
- 가장 많은 연산량을 요구

'CS' 카테고리의 다른 글
| [CS] 트랜젝션 (0) | 2023.01.28 |
|---|---|
| [CS] OSI 7 계층 (0) | 2023.01.28 |
| [CS] 프로세스와 스레드 (0) | 2023.01.26 |
| 리액티브 프로그래밍(Reactive Programming) (0) | 2023.01.13 |
| 객체지향 5원칙 SOLID (0) | 2023.01.10 |
![[CS] 해시(Hash)와 해시 충돌 해결 방법](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FwGZIm%2FbtrXnk8HYxc%2FpQSlASBLvTsniPJD4uz7jk%2Fimg.png)