자료구조란
- 데이터 값들을 저장하거나 조직하는 방법.
- 각 원소들이 논리적으로 정의된 규칙에 의해 나열되며 자료에 대한 처리를 효율적으로 수행할 수 있도록 자료를 구분하여 표현한 것.
- 연산에 사용되는 컴퓨터의 메모리 자원은 매우 한정적인데 반해 처리해야 할 데이터는 무수히 많을 수 있다. 따라서 이 메모리 공간을 효율적으로 사용해야 하는데 필요한 것이 자료 구조이다.
- 효율적인 자료 구조의 선택 → 효율적인 알고리즘의 선택이 된다.

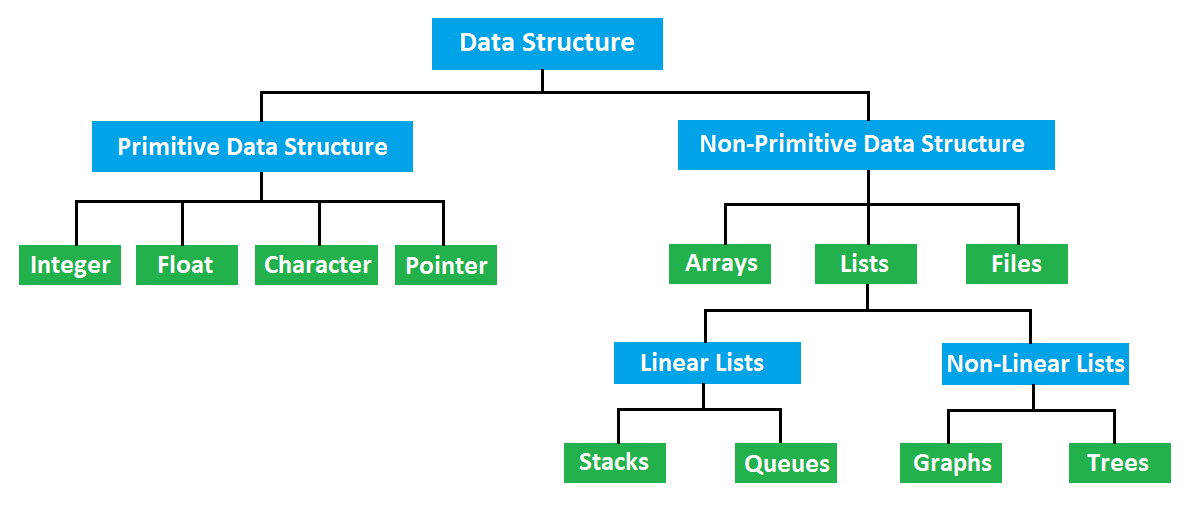
1) 단순 구조(Primitive Data Structure)
- 프로그래밍에서 사용되는 기본 데이터 타입
- Javascript에는 6개의 원시 타입(Number, String, Boolean, null, undefined, Symbol)이 있다. (Symbol - ES6 버전의 JavaScript에서 새롭게 추가)
2) 비단순 구조(Non-Primitive Data Structure) / 참조타입(Reference data type)
- 여러 데이터를 목적에 맞게 효과적으로 저장하는 자료 구조. (자바스크립트에선 원시 자료형이 아닌 모든 것은 참조 자료형이다)
- 배열([])과 객체({}), 함수(function(){})가 대표적이다.
- 참조 자료형을 변수에 할당할 때는 변수에 값이 아닌 주소를 저장한다.
- 동적으로 크기가 변하는 데이터를 보관하기위해 변수가 아닌 다른곳에 데이터를 저장하고 변수에는 그 주소만 할당한다.
3) 선형 구조(Linear Data Structure)
- 저장된 자료의 전후 관계가 1:1인 경우
4) 비선형 구조(Non-Linear Data Structure)
- 데이터 항목 사이의 관계가 1:n인 경우
1. Array (배열)

- 배열은 대부분의 프로그래밍 언어에서, 가장 간단하고 가장 많이 쓰이는 자료구조형이다.
- 자료들이 메모리 주소(선반)에 순서대로 정렬되어 있기 때문에 논리적 순서와 물리적 순서가 일치한다. 따라서 index값을 통한 원소의 직접 접근이 용이하며, 구현이 쉽다.
- 특정 데이터를 순차적으로 iterate해야 하는 경우 배열은 최상의 자료구조형이다.
- 단점으로는 삽입, 삭제 등에 대한 연산에 필요한 Cost가 높다는 것이다. 삭제의 경우 순서를 맞추기 위해, 뒤의 원소들을 모두 앞으로 Shift연산을 해줘야 하며, 삽입의 경우도 삽입한 인덱스 포함, 그 뒤의 인덱스들에 Shift 연산을 해줘야 한다.
- Random Access를 지원한다.
- 시간복잡도는 특정 요소에 접근하는 경우 O(1) / 삽입과 삭제시 O(N)이 소요된다.
2. LinkedList

- 배열의 삽입/삭제 연산에 대한 비효율성을 극복하고자 등장한 것이 LinkedList 이다.
- Array와 LinkedList의 차이점은 LinkedList는 논리적으론 순서대로 되어있으나 물리적으론 순서대로 되어있지 않다. 대신 LinkedList는 각 원소가 다음 index 위치에 해당하는 물리적 주소를 가지고 있다. 그렇기에 삽입/삭제시에는 데이터를 Shift할 필요 없이, 해당되는 원소의 물리적 주소만 변경해주면 된다.
- 위와 같은 특징 때문에 특정 index를 참조하려면, 1번 index부터 차례대로 접근해야 한다는 비효율성이 있다.
- 시간복잡도는 특정 요소에 접근하는 경우 O(N) / 삽입과 삭제시 O(1)이 소요된다.
3. Stack (스택)

- Stack 은 선형 자료구조의 일종으로, LIFO(Last In First Out)의 대표적인 예시로 들 수 있다.
- 말 그대로 나중에 들어간 것이 먼저 나오는 구조.
- 브라우저 히스토리(이전 페이지, 다음 페이지) 또는 ctrl+z로 이전 작업을 취소하는 등의 동작에 쓰이는 자료구조이다.
- 스택과 큐는 자바스크립트에 내장되어 있지 않으므로, 사용을 원하면 스스로 구조를 만들어야 한다.
- 구조 생성시 비교 -
- Array의 장점 : 각 element들이 서로 연관되어 있기 때문에 속도가 더 빠르다. 하지만 메모리 공간이 한정되어 있기 때문에 할당된 메모리를 다 사용하면 현재 배열을 다른 곳에 복사하기 때문에 메모리를 조금 더 사용하게 될 수도 있다.
- Linked List의 장점 : 메모리 여기저기에 흩어져있기 때문에 상대적으로 느릴 수 있다. 하지만 반면 메모리 공간이 한정되어 있지 않고 얼마든지 계속 값을 추가할 수 있다는 장점이 있다.
4. Queue (큐)
- 먼저 도착한 사람이 먼저 입장하는 FIFO(First In, First Out) 개념이다.
- 레스토랑 앱, 예매 앱, 작업 우선순위, Heap 구현 등에 사용된다.
- 장점 : Fast Operation(removing, pushing), Fast Peek, Ordered
- 단점 : Slow Lookup
- 구조를 생성시 array로 만들면 좋지 않다. Array의 경우 앞에서부터 element를 제거해야 하는데 그 경우 index를 다시 재조정해야 하기 때문에 O(n)이 된다. 따라서 Queue는 반드시 Linked List로 만든다.
5. Hash Table (해시 테이블)
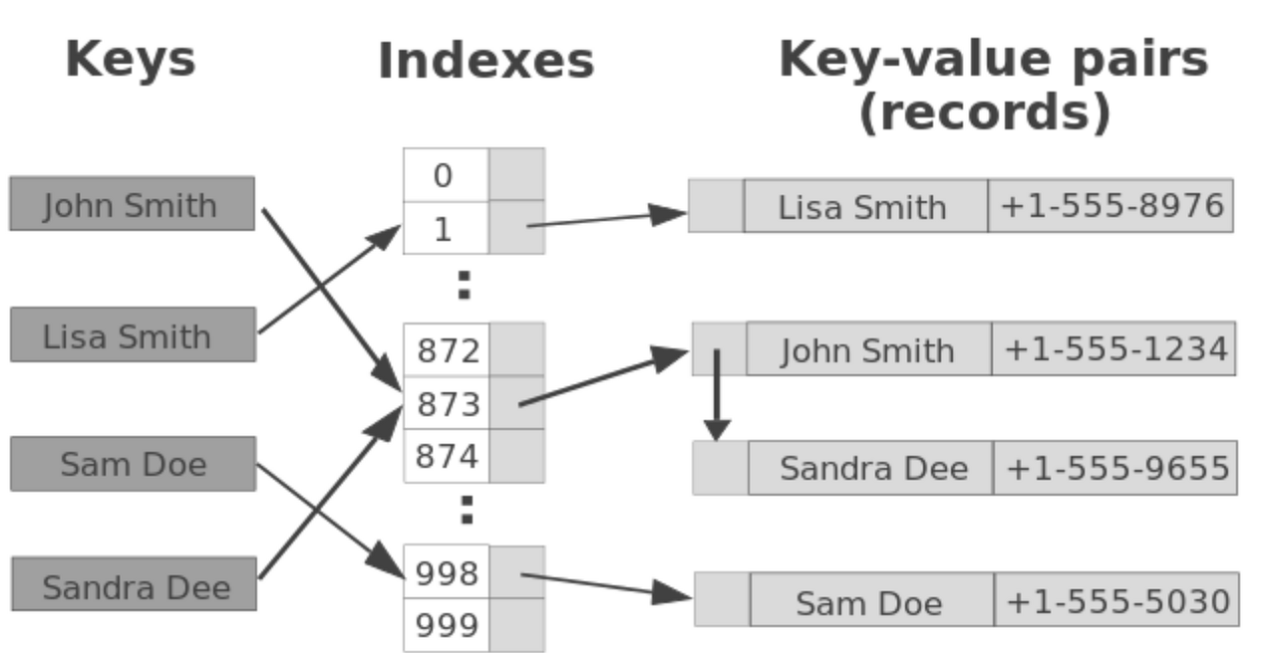
- Hash Table은 Key와 Value가 쌍을 이룬 형태로 데이터가 저장되어 있는 자료구조형을 지칭한다.
- JS에서 해시테이블은 대표적으로 Object, Map, Set이 있다.
- 배열 내 데이터도 Key와 Value로 이루어져 있기는 하나, Key가 오직 index 숫자만 가능한 것에 비해 Hash Table에서는 문자열 또한 Key가 될 수 있다.
- 내부적으로 배열을 사용하며, 평균적으로 빠른 탐색속도(O(1))를 갖는다.
- 장점
- Fast Search : 배열은 전체를 순회하며 값을 찾아야 하는 반면, 해쉬 테이블은 key를 통해 바로 찾고자 하는 값에 접근이 가능하다.
- Fast Insertion and Deletion : 해쉬 테이블은 데이터가 정렬되어 있지 않기 때문에, 바로 값을 추가하고 지울 수 있다.
- Fast lookup : 배열과 객체 모두 index 또는 key를 알고 있으면 되므로 lookup도 빠르다.
- 단점
- 무작위 주소 할당으로 인한 문제.
6. 트리(Tree)
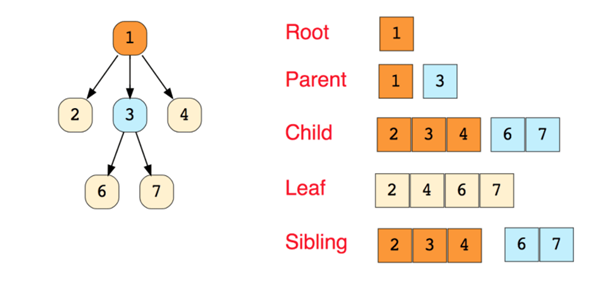
- Stack, Queue와는 다르게 비선형 자료구조로, 계층적 구조를 표현하는 자료구조이다.
- Node (노드) : 트리를 구성하고 있는 원소 그 자체를 말한다.
- Edge (간선) : 노드와 노드사이를 연결하고 있는 선을 말한다.
- Root(Node) : 트리에서 최상위 노드를 말한다.
- Terminal(Node) : 트리에서 최하위 노드를 말한다. Leaf Node라고도 한다.
- Internal(Node) : 트리에서 최하위 노드를 제외한 모든 노드를 말한다.
Binary Tree (이진트리)
- Binary Tree는 Root 노드를 포함, Leaf 노드를 제외한 모든 노드의 자식이 두 개인 것을 말한다. 공집합 역시 노드로 인정한다. 노드로 이루어진 각 층을 Level이라 하며, Level의 수를 이 트리의 height라 한다.
- 이진트리에는 모든 Level이 가득 찬 이진 트리인 Full Binary Tree(포화 이진 트리) 와 위에서 아래로, 왼쪽에서 오른쪽으로 순서대로 채워진 트리인 Complete Binary Tree(완전 이진 트리) 가 있다. 배열로 포화 이진트리와 완전 이진트리를 구현했을 때, 노드의 개수 n에 대해서 i번째 노드에 대해서 parent(i) = i/2 , left_child = 2i, right_child = 2i + 1 의 인덱스 값을 갖는다.
7. Graph

- 각 노드들이 서로 연결되어 있는 자료 구조형으로, 아주 커다란 자료 구조형의 범위 중 하나이다.
- 실제로 그래프 자료 구조 안에 Trees 자료구조가 포함되어 있고, Trees 안에는 Linked List가 포함되어 있다. 즉, 그래프는 이들을 모두 포괄하고 있는 자료 구조형인 것이다.
- Undirected와 Directed Graph가 있고, 방향성 유무로 결정된다.
- Undirectd Graph에서 Degree란 정점에 연결된 간선의 개수이다.
- Directed Graph에서의 Degree는 방향성이 있기 때문에 둘로 나뉘는데, 나가는 간선의 개수는 Outdegree, 들어오는 간선의 개수를 Indegree라 한다.
- 가중치 그래프 란 간선에 가중치를 둔 그래프이며, 부분 그래프란 한 그래프의 일부 정점 및 간선으로 이루어진 그래프이다.
그래프의 구현 방법 :
인접 행렬 : 정방 행렬을 사용하여 구현. 연결 관계를 O(1)로 파악 가능. 공간 복잡도는 O(2V)
인접 리스트 : 리스트를 사용하여 구현. 정점간 연결 여부 파악애 오래 걸림. 공간 복잡도는 O(E + V)
탐색 방법에는 깊이 우선 탐색(DFS, Depth First Search)와 너비 우선 탐색(BFS, Breadth First Search)이 있다.
깊이 우선 탐색은 말 그대로 깊숙히 들어가서 탐색하고 나오는 것이며, 유용한 자료구조는 Stack이다.
너비 우선 탐색은 임의의 한 정점에 대해 인접한 정점을 queue에 넣고(enqueue), dequeue연산에서 나온 하나의 정점으로 들어가서 그 정점의 인접한 정점을 다시 Queue에 넣어서 탐색하는 방식. BFS로 찾은 경로는 최단 경로이다.
본 게시물은 여러 사이트 및 블로그, 백과사전을 참고 하였습니다.
학습을 위하여 여러 내용들을 직접 타이핑하며 필요한 내용들만 요약하였습니다.
틀린 내용이나 압축된 내용이 있을 수 있습니다.
해당 부분에 대해선 학습을 더 진행하며 보완할 예정입니다.
끝까지 읽어주셔서 감사합니다.
'Javascript' 카테고리의 다른 글
| [node.js] JavaScript heap out of memory (0) | 2023.08.29 |
|---|---|
| [TypeScript] 추상 클래스(Abstract Class) (0) | 2023.01.28 |
| [Javascript] Lazy evaluation(지연 평가) (0) | 2023.01.19 |
| [Javascript] Generator Function (0) | 2023.01.19 |
| [Javascript] 커링(Currying)이란 (0) | 2023.01.17 |
![[Javascript] 자료구조 (Data Structure)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fbe6deU%2FbtrWRWU7X6G%2FAAAAAAAAAAAAAAAAAAAAAFoFeqCaInNa3cpphVgiagZOUvq4Qu0NmaLZDvSMm8NX%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DVqOwXh6uWAnXunTuNDmXcGGLNK8%253D)